编译 | 禾木木

出品 | AI科技大本营（ID:rgznai100）

现在小学生的数学题不能用简单来形容，有的时候家长拿到题也需要思考半天，看看是否有其他隐含的解题方法。市面上更是各种拍题搜答案的软件，也是一样的套路，隐含着各种氪金的信息。

就像网络上说的“不写作业母慈子孝，一写作业鸡飞狗跳”。

近日，OpenAI 训练了一个新系统，可以解决小学数学题，大大提升了 GPT-3 的逻辑推理问题。

新系统可以解决小学数学问题，60 亿参数的 GPT-3 采用“新方法”，准确率直接翻倍！甚至追平了拥有 1750 亿参数，采用微调方法的 GPT-3 模型。

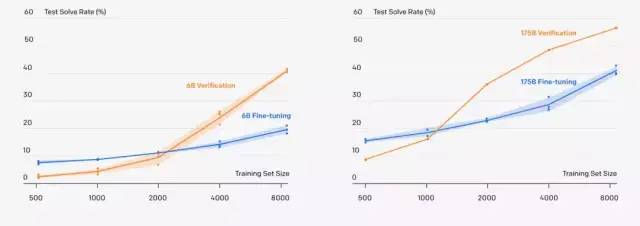
还有一项重要的结果是，一个9-12岁的小学生在测试中得分为60分，采用新方法的GPT-3在同样的问题上可以拿到55分，已经达到了小学生90%左右的水平！

训练验证器

GPT-3 之前就有说过许多令人印象深刻的技能，像是模仿人的多种写作风格、20分钟内完成论文、在文本生成上与人类写作相媲美等。然而，他们却很难执行准确多步推理的任务，例如小学数学题。尽管类似这样的模型可以推导出正确解决方案大致内容，但也经常会产生严重的逻辑错误。

为了在复杂逻辑领域可以达到与人类相媲美的性能，模型必须具有判别自身错误的能力，并谨慎地执行之后的过程。

为此，OpenAI 的研究者提出了一个训练验证器（verifier）来判断模型完成的正确性。

在测试阶段会生成许多候选解决方案并选择排名最高的一个。证明验证（verification）显着提高了 GSM8K 的性能，此外也为这一观点（随着数据的增加，验证比微调基线更有效）提供了强有力证据。

验证器具体训练方法分为三步：

先把模型的「生成器」在训练集上进行2个epoch的微调。

从生成器中为每个训练问题抽取100个解答，并将每个解答标记为正确或不正确。

在数据集上，验证器再训练单个epoch。

生成器只训练2 个epoch 是因为2个 epoch 的训练就足够学习这个领域的基本技能了。如果采用更长时间的训练，生成的解决方案会过度拟合。

测试时，解决一个新问题，首先要生成100个候选解决方案，然后由「验证器」打分，排名最高的解决方案会被最后选中。

微调

OpenAI 通过更新模型参数来进行微调，以最小化所有训练 token 的交叉熵损失。

结果很显然，可以看到 175B 模型明显优于较小的模型。

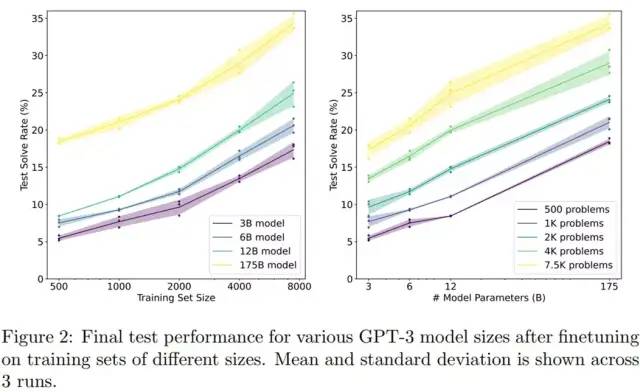
假设一个对数线性趋势，当使用完整的 GSM8K 训练集时，需要具有 10^16 个参数的模型才能达到 80% 的求解率。尽管如此，175B 模型似乎需要至少两个额外数量级的训练数据才能达到 80% 的求解率。

在下图中，OpenAI 展示了 6B 模型测试性能在 100 个训练 epoch 的过程中如何变化。

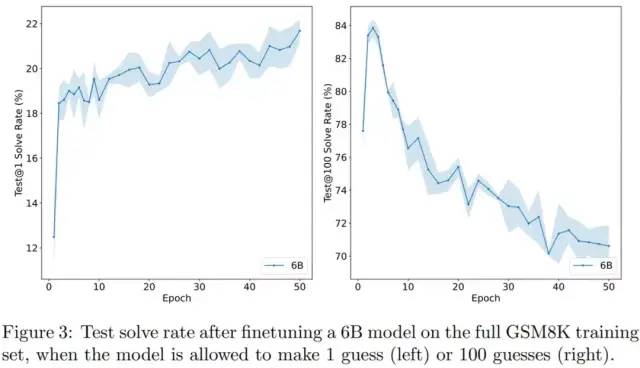
当允许模型对每个问题进行 N 个单独的猜测时，OpenAI 使用 test@N 表示至少一次正确解决的问题的百分比。

尽管很快开始过拟合测试损失，但 Test@1 的性能几乎单调地提高。并且，随着 epoch 次数的增加，test@100 的性能比 test@1 下降得更快。

选择具有良好覆盖性的模型对于成功训练验证器至关重要。

从实证角度来看，test@100 性能在前几个 epoch 内达到峰值。出于这个原因，OpenAI 使用训练了 2 个 epoch 的模型来生成用于训练验证器的样本。如果改为微调 6B 模型以直接输出最终答案而无需任何中间步骤，则性能会从 20.6% 急剧下降至 5.2%。

GSM8K 数据集

OpenAI 基于四个设计原则创建了 GSM8K 数据集：高质量、高多样性、中等难度和自然语言解决方案。

高质量：GSM8K中的问题都是人工设计的，避免了错误问题的出现。

高多样性：GSM8K中的问题都被设计得相对独特，避免了来自相同语言模板或仅在表面细节上有差异的问题。

中等难度：GSM8K中的问题分布对大型SOTA语言模型是有挑战的，但又不是完全难以解决的。这些问题不需要超出早期代数水平的概念，而且绝大多数问题都可以在不明确定义变量的情况下得到解决。

自然语言解决方案：GSM8K中的解决方案是以自然语言而不是纯数学表达式的形式编写的。模型由此生成的解决方案也可以更容易被人理解。此外，OpenAI也期望它能阐明大型语言模型内部独白的特性。

GSM8K 数据集由 8.5K 个高质量小学数学应用题组成。每个问题需要 2 到 8 步解决，解决方案主要涉及使用加减乘除等基本算术运算执行一系列基础计算以获得最终答案。微调后的 SOTA 模型在该数据集上表现不佳，主要是问题的高度多样性导致的。与此同时，GSM8K 解决方案仅依赖于基本概念，因此实现高测试性能是一个容易实现的目标。

GSM8K 数据集中的三个示例问题

值得注意的是，GSM8K 中的解决方案是用自然语言而不是纯数学表达式编写的。通过坚持使用自然语言，模型生成的解决方案更容易被人类解释。OpenAI 的方法保持相对领域不可知。

在GSM8K数据集上，OpenAI测试了新方法验证（verification）和基线方法微调（fine-tuning）生成的答案。

案例展示：

问题：Tim 种了 5 棵树。他每年从每棵树上收集 6 个柠檬。他十年能得到多少柠檬？

175B Verification：正确

175B Fine-tuning：错误

6B Verification：正确

6B Fine-tuning：错误

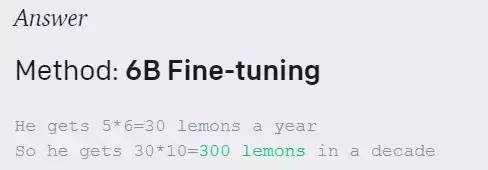
很明显，验证方法比基线方法（微调）在回答数学题有了很大的提升。

对于这两种方法，OpenAI 使用 GPT-3 系列模型作为初始化，主要关注 175B 和 6B 大小的模型。175B 模型最大，产生的结果最令引人瞩目，而 6B 模型更易于实现研究目。

结论

通过 OpenAI 所展现出的数学实例可以看出，使用验证方法比单纯扩大参数要更加智能，但缺点是并不稳定。

现下，通过在一些简单的领域试验新路径，识别和避免机器学习的错误是推动模型发展的关键方法，比如简单的小学数学题。最终当我们试图将模型应用到逻辑上更复杂的领域时，那些不被了解的技能将变得越来越透明。

参考链接：

https://openai.com/blog/grade-school-math/

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。