来源 | 知乎CVer计算机视觉专栏

我们基于FCOS，首次在dense prediction上利用全卷积结构做到E2E，即无NMS后处理。我们首先分析了常见的dense prediction方法（如RetinaNet、FCOS、ATSS等），并且认为one-to-many的label assignment是依赖NMS的关键。受到DETR的启发，我们设计了一种prediction-aware one-to-one assignment方法。此外，我们还提出了3D Max Filtering以增强feature在local区域的表征能力，并提出用one-to-many auxiliary loss加速收敛。我们的方法基本不修改模型结构，不需要更长的训练时间，可以基于现有dense prediction方法平滑过渡。我们的方法在无NMS的情况下，在COCO数据集上达到了与有NMS的FCOS相当的性能；在代表了密集场景的CrowdHuman数据集上，我们的方法的recall超越了依赖NMS方法的理论上限。

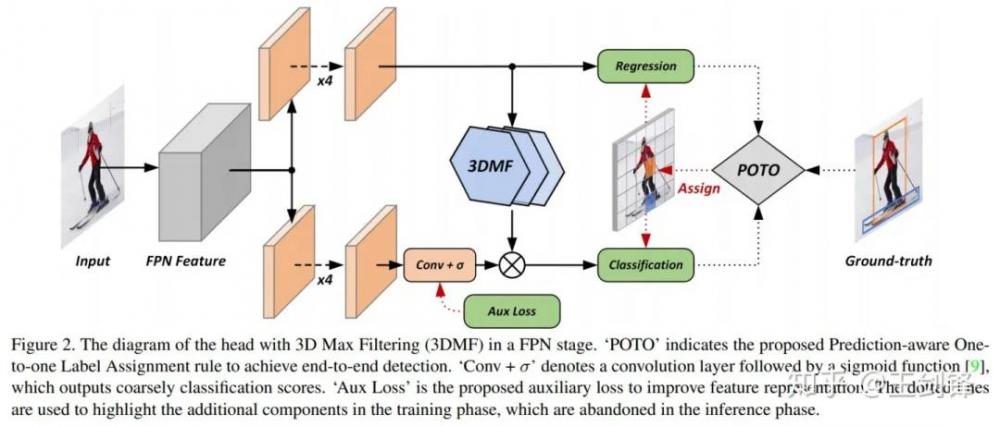
整体方法流程如下图所示：

One-to-many vs. one-to-one

自anchor-free方法出现以来，NMS作为网络中最后一个heuristic环节，一直是实现E2E dense prediction的最大阻碍。但其实我们可以发现，从RPN、SSD、RetinaNet等开始，大家一直遵循着这样一个流程：先对每个目标生成多个预测（one-to-many），再将多个预测去重（many-to-one）。所以，如果不对前一步label assignment动刀，就必须要保留去重的环节，即便去重的方法不是NMS，也会是NMS的替代物（如RelationNet，如CenterNet的max pooling）。

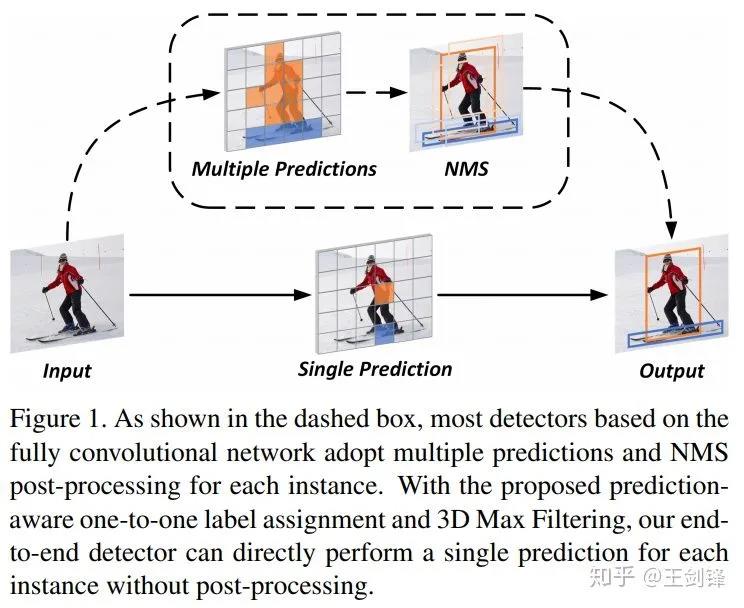
那直接做one-to-one assignment的方法是否存在呢？其实是有的。上古时代有一个方法叫MultiBox，对每个目标和每个预测做了bipartite matching，DETR其实就是将该方法的网络换成了Transformer。此外还有一个大家熟知的方法：YOLO，YOLO也是对每个目标只匹配一个grid[1]，只不过它是采用中心点做的匹配，而且有ignore区域。

Prediction-aware one-to-one

于是接下来的问题就是，在dense prediction上我们能不能只依赖one-to-one label assignment，比较完美地去掉NMS？我们首先基于去掉centerness分支的FCOS，统一网络结构和训练方法，用Focal Loss + GIoU Loss，做了如下分析实验：

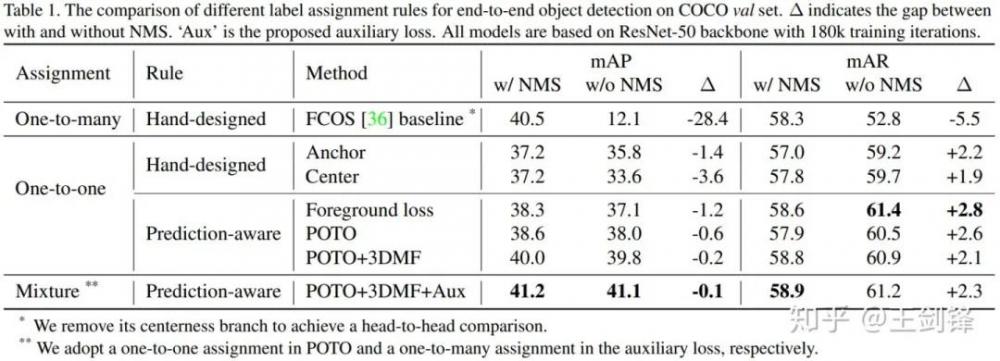
我们设计了两种hand-crafted one-to-one assignment方法，分别模仿RetinaNet（基于anchor box）和FCOS（基于center点），尽可能做最小改动，发现已经可以将有无NMS的mAP差距缩小到4个点以内。

但我们认为手工设计的label assignment规则会较大地影响one-to-one的性能，比方说center规则对于一个偏心的物体就不够友好，而且在这种情况下one-to-one规则会比one-to-many规则的鲁棒性更差。所以我们认为规则应该是prediction-aware的。我们首先尝试了DETR的思路，直接采用loss做bipartite matching的cost[2]，发现无论是绝对性能还是有无NMS的差距，都得到了进一步的改善。

但我们知道，loss和metrics往往并不一致，它常常要为优化问题做一些妥协（比如做一些加权等等）。也就是说，loss并不一定是bipartite matching的最佳cost。因而我们提出了一个非常简单的cost：

看起来稍微有点复杂，但其实就是用网络输出的prob代表分类，网络输出和gt的IoU代表回归，做了加权几何平均，再加一个类似于inside gt box的空间先验。加权几何平均和空间先验我们后面都分别做了ablation。

这就是我们提出的POTO策略，它进一步地提升了无NMS下的性能，也侧面验证了loss并不一定是最好的cost[3]。但从Table 1中我们也发现了，POTO的性能依旧不能匹敌one-to-many+NMS组合。我们认为问题出在两个方面：

1、one-to-one需要网络输出的feature非常sharp，这对CNN提出了较严苛的要求（这也是Transformer的优势）；

2、one-to-many带来了更强的监督和更快的收敛速度。

我们分别用3D Max Filtering和one-to-many auxiliary loss缓解如上问题。

3D Max Filtering

针对第一点，我们提出了3D Max Filtering，这基于一个intuition（paper中没有提到）：卷积是线性滤波器，学习max操作是比较困难的。此外，我们在FCOS上做了实验，发现duplicated predictions基本来自于5×5的邻域内，所以最简单的做法就是在网络中嵌入最常见的非线性滤波器max pooling。另外，NMS是所有feature map一起做的，但网络在结构上缺少层间的抑制，所以我们希望max pooling是跨层的。

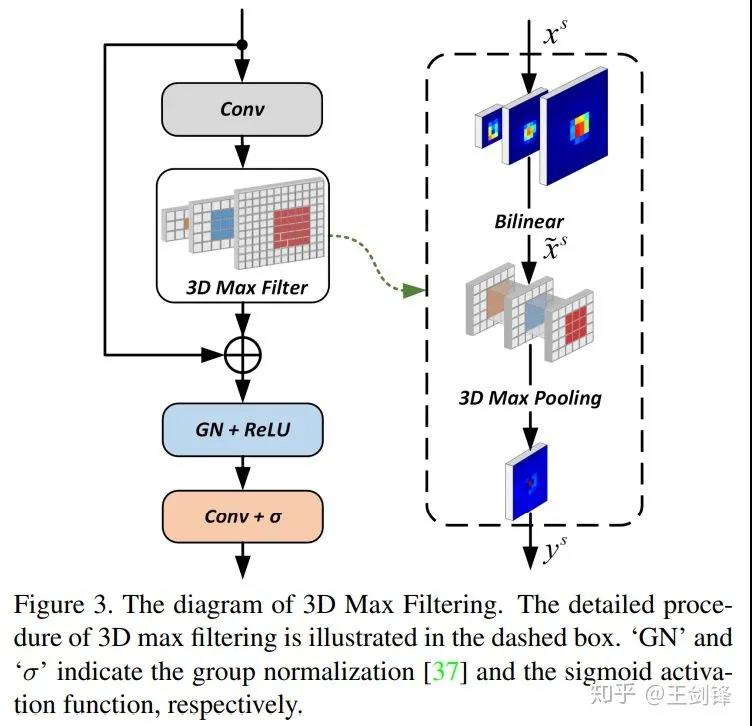
如Figure 3所示，这个模块只采用了卷积、插值、max pooling 3d，速度非常快，也不需要写cuda kernel。

One-to-many auxiliary loss

针对第二点监督不够强、收敛速度慢，我们依旧采用one-to-many assignment设计了auxiliary loss做监督，该loss只包含分类loss，没有回归loss。assignment本身没什么可说的，appendix的实验也表明多种做法都可以work。这里想提醒大家的是注意看Figure 2的乘法，它是auxiliary loss可以work的关键。在乘法前的一路加上one-to-many auxiliary loss，乘法后是one-to-one的常规loss。由于1*0=0，1*1=1，我们只需要大致保证one-to-one assignment的正样本在one-to-many中依然是正样本即可。

实验

最主要的实验结果已经在Table 1中呈现了，此外还有一些ablation实验。

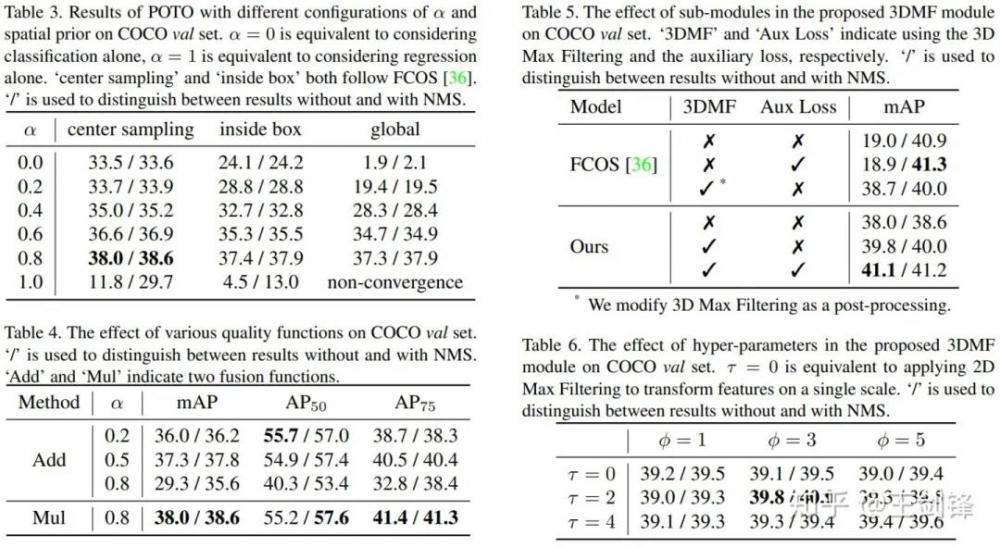
这里highlight几点：

1、α越低，分类权重越大，有无NMS的差距越小，但绝对性能也会降低[4]；α太高也不好，我们后续所有实验用α=0.8；

2、在α合理的情况下，空间先验不是必须的，但空间先验能够在匹配过程中帮助排除不好的区域，提升绝对性能；我们在COCO实验中采用center sampling radius=1.5，在CrowdHuman实验中采用inside gt box[5]；

3、加权几何平均数（Mul）[6]比加权算术平均数（Add）[7]更好。

去掉NMS的最大收益其实是crowd场景，这在COCO上并不能很好地体现出来。所以我们又在CrowdHuman上做了实验如下：

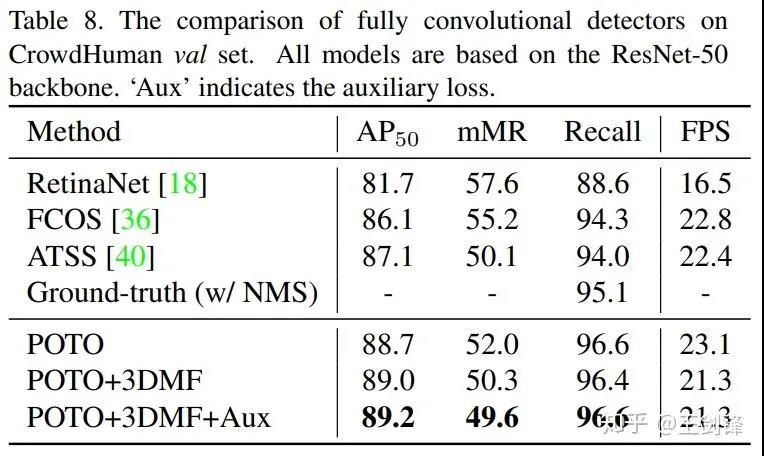
请注意CrowdHuman的ground-truth做NMS threshold=0.6，只有95.1%的Recall，这也是NMS方法的理论上限。而我们的方法没有采用NMS，于是轻易超越了这一上限。

我们还做了其它一些实验和分析，欢迎看原文。

可视化

经过以上改进，我们成功把one-to-one的性能提升到了与one-to-many+NMS方法comparable的水平。我们可视化了score map，可以发现FCN是有能力学出非常sharp的表示的，这也是很让我们惊奇的一点。

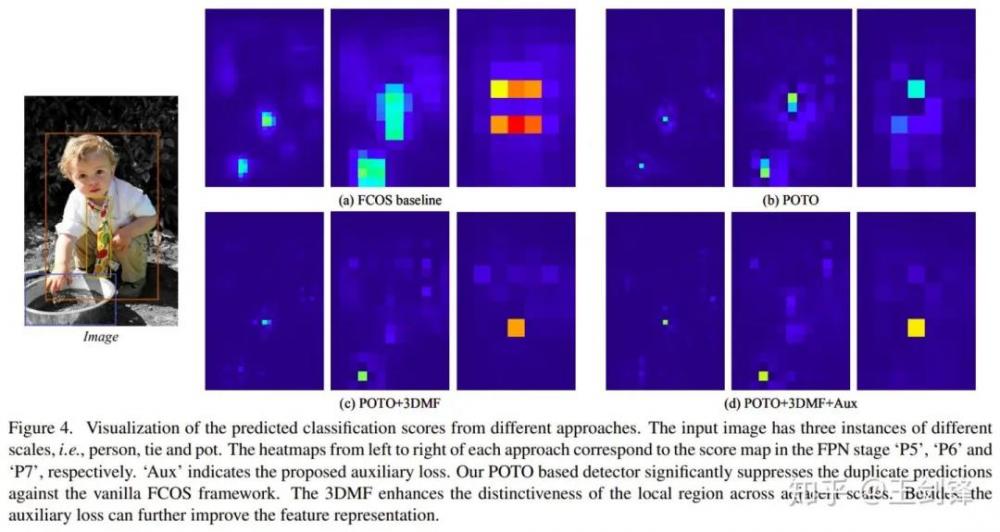
结果图中比较明显的改善出现在多峰case上。比如两个物体有一定的overlap（但又没有特别重合），这个时候one-to-many+NMS方法经常出现的情况是，除了两个物体分别出了一个框之外，在两个物体中间也出了一个框，这个框与前两个框的IoU不足以达到NMS threshold，但置信度又比较高。这类典型的多峰问题在POTO中得到了较大的缓解。

Others

有些人可能比较关心训练时间，因为潜意识里在dense prediction上做bipartite matching应该是很慢的。然而实际上依赖于scipy对linear_sum_assignment的优化，实际训练时间仅仅下降了10%左右。

如果对这一时间依然敏感，可以用topk（k=1）代替bipartite matching；在dense prediction里top1实际上是bipartite matching的近似解[8]。相似地，k>1的情况对应了one-to-many的一种新做法，我们组也对此做了一些工作，后续可能会放出来。

顺便打一波广告：对旷视研究院BaseDetection组感兴趣的同学可以发简历到wangjianfeng@megvii.com，组里目前主要在做目标检测、自监督等方向。

参考

1.如果有人感兴趣的话，可以在YOLO上去掉NMS尝试一下，可以接近30mAP。

2.注意我们这里没有使用DETR的CE+GIoU+L1组合，而是直接采用loss本身（Focal+GIoU）。我们认为这样更符合DETR用loss做cost的原意。

3.其实这里可以有一个脑洞留给大家，因为cost是不需要求导的，所以甚至是可以直接算AP当cost的。

4.侧面印证了分类和回归的冲突在检测任务上是显著的。

5.理由很简单，CrowdHuman的遮挡问题太严重，center区域经常完全被遮挡。

6.事实上加权几何平均数的负对数就是CE+IoU Loss，加权算术平均数则没有明显的物理含义。

7.NoisyAnchor在assign中采用了类似的公式，只不过采用的是anchor IoU。

8.更具体来讲，top1（即argmin）是Hugarian Algorithm只做第一次迭代的结果；由于在dense prediction下冲突会很少，一次迭代就已经逼近了最优匹配，这也是为什么Hungarian Algorithm这里实际运行很快。

链接：

https://link.zhihu.com/?target=https%3A//arxiv.org/abs/2012.03544

代码：

github.com/Megvii-BaseD（内部代码迁移+审查中，后续放出）

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。